Phương pháp giải ngược (Backsolving)
Phương pháp giải ngược (Backsolving) sẽ giúp các em giải quyết các bài toán một cách nhanh chóng, đặc biệt là các bài toán đại số phức tạp. Chúng ta sẽ làm ngược từ dưới lên, có nghĩa là tận dụng chính các phương án mà đề bài cung cấp để tìm ra lời giải đúng cho bài toán. Phương pháp này giúp tiết kiệm thời gian và giúp các em nhanh chóng loại bỏ các lựa chọn sai. Sau đây là một bài toán có thể xuất hiện trong đề thi thật:
The equation 3x – 2 = 8 - 2x has the solution x = _____.
(A) 1
(B) 2
(C) 3
(D) 4
Bây giờ chúng ta sẽ chọn một phương án bất kỳ để thay số vào phương trình ở đề bài
- Chúng ta sẽ bắt đầu với phương án (C) 3. Khi x = 3 thì vế trái của phương trình là 3 x 3 – 2 = 7, trong khi vế phải là 8 – 2 x 3 = 2 -> Không thỏa mãn phương trình.
- Chúng ta sẽ tiếp tục với phương án (B) 2. Khi x = 2 thì vế trái của phương trình là 3 x 2 – 2 = 4, trong khi vế phải là 8 – 2 x 2 = 4 -> Thỏa mãn phương trình.
Vậy đáp án đúng là B!
Phương pháp thay số
Phương pháp thay số sẽ giúp các em giải quyết dễ dàng các bài toán xuất hiện nhiều biến số. Chúng ta sẽ gán các giá trị ngẫu nhiên cho các biến số xuất hiện trong đề bài sao cho chúng thỏa mãn yêu cầu đề bài và sử dụng các giá trị đó để thực hiện yêu cầu đề bài đưa ra. Sau đây là một bài toán có thể xuất hiện trong đề thi thật:
If a + b = c, which of the following is equal to a2 + b2?
A. c + 2ab
B. c2
C. c2 – ab
D. c2 – 2ab
Chúng ta có thể bắt đầu giải bài toán bằng cách cho a = 2 và b = 3. Đề bài cho chúng ta biết rằng c là tổng của a và b, vậy c = 2 + 3 = 5. Tiếp tục sử dụng các dữ kiện đó, chúng ta có a2 + b2 = 22 + 32 = 4 + 9 = 13.
Tiếp theo đó, chúng ta sẽ thay các giá trị của a,b,c vào 4 phương án A,B,C,D:
A. c + 2ab = 5 + 2 x 2 x 3 = 5 + 12 = 17
B. c2 = 52 = 25
C. c2 – ab = 52 – 2 x 3 = 25 – 6 = 19
D. c2 – 2ab = 52 – 2 x 2 x 3 = 25 – 12 = 13
Vậy đáp án đúng là D!
Cách sử dụng graphing calculator
Graphing calculator là một công cụ vô cùng hữu hiệu giúp các em hình dung và phân tích các hàm số, đặc biệt là hàm số bậc hai và hàm số mũ. Graphing calculator giúp các bài toán phức tạp trở nên đơn giản hơn rất nhiều. Sau đây là một bài toán có thể xuất hiện trong đề thi thật:
The graph of a quadratic equation is a parabola. Find the vertex of the parabola represented by the equation y = x
2 + 4x + 3.
Bây giờ chúng ta sẽ sử dụng graphing calculator được tích hợp sẵn trong giao diện bài thi để vẽ đồ thị hàm số y = x2 + 4x + 3. Sau khi nhập đầy đủ hàm số vào máy tính, ta thu được đồ thị như sau:
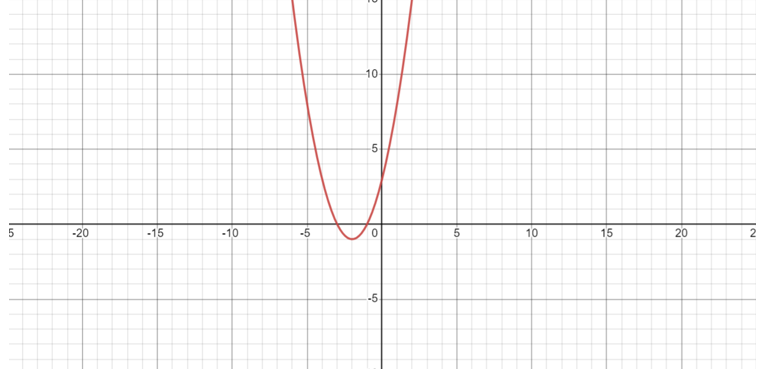
Sau đó, chúng ta bấm vào điểm thấp nhất để tìm ra tọa độ của đỉnh đồ thị:
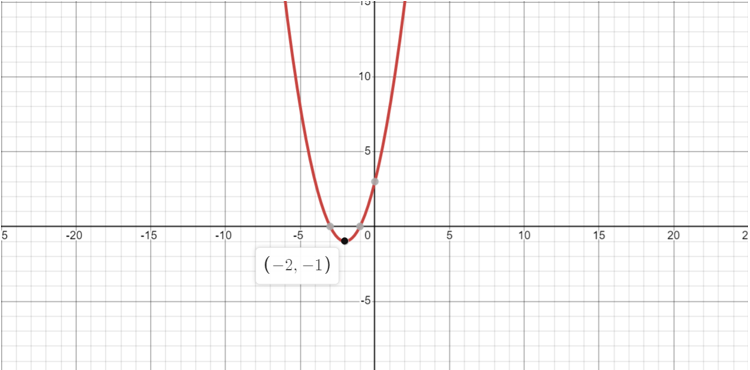
Vậy đỉnh của đồ thị y = x
2+ 4x + 3 là (-2, -1)!
Sử dụng nhiều cách giải cho một bài toán
Sử dụng nhiều cách giải khác nhau cho cùng một bài toán là một mẹo hữu hiệu để các em kiểm tra lại bài xem liệu kết quả chúng ta tìm ra có phải là kết quả chính xác hay không. Đây là một câu hỏi có thể xuất hiện trong đề thi thật:
Find the roots of the quadratic equation 2x
2 - 5x + 2 = 0.
Cách 1: Đưa vế trái về dạng nhân tử
2x
2 – 5x + 2 = 0
2x
2 – 4x – x + 2 = 0
2x(x – 2) – (x – 2) = 0
(2x – 1)(x – 2) = 0
2x – 1 = 0 hoặc x – 2 = 0
Vậy nghiệm của phương trình là x = ½ và x = 2.
Sau khi giải theo cách 1, chúng ta có thể giải theo một cách khác để kiểm tra lại bài:
Cách 2: Sử dụng graphing calculator
Chúng ta sẽ nhập phương trình hàm số y = 2x
2 - 5x + 2 vào giao diện của graphing calculator và tìm các giao điểm của đồ thị hai hàm số y = 2x
2 - 5x + 2 và y = 0 (hay nói cách khác là trục Ox).
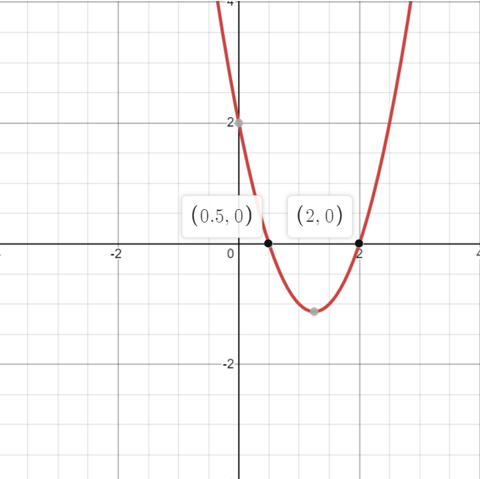
Giao điểm của hai đồ thị là hai điểm (0.5, 0) và (2, 0).
Vậy nghiệm của phương trình là x = ½ và x = 2.
Chúng ta thấy rằng hai cách làm đều đưa tới kết quả giống nhau, vậy chúng ta đã làm ra kết quả đúng!
Bài tập
Bài 1:
In a certain office, there are c chairs, d desks, and e employees. Five desks are not occupied, and all other desks are occupied by exactly one employee. All but two of the employees have two chairs at their desks, and all the other desks, whether they are occupied or not, have one chair. If e > 2 then which of the following expressions is equal to c?
A) 2(d - 5) + e
B) 2(d - e)
C) 2(d - 2)
D) 2e + 3
Bài 2:
Rajesh sells only hats and scarves at his store, for which he charges $13 and $7, respectively. On Monday, he sold 15 items and made $123. How many hats did Rajesh sell on Monday?
A) 3
B) 4
C) 5
D) 6
.png)
Kết luận
Bằng cách kết hợp phương pháp giải ngược, thay số và graphing calculator, các em có thể nâng cao khả năng giải quyết các bài toán và tham gia kỳ thi một cách tự tin. Hãy nhớ luyện tập những phương pháp này thường xuyên và quản lý thời gian một cách hiệu quả. Với sự chuẩn bị kỹ càng, các em chắc chắn sẽ giải quyết thành công những bài toán Toán khó trong bài thi SAT. Chúc các em may mắn!
Group Facebook
Để biết thêm nhiều thông tin bổ ích về bài thi SAT Digital, các em hay tham gia ngay nhóm "Học SAT cô Vân Anh" trên Facebook nhé. Nhấn vào
đây để tham gia nhóm ngay thôi nào.







.png)

Trần Đình Quang (1560 SAT, THPT Chuyên Khoa Học tự nhiên) Trải nghiệm học SAT với TOEFL, con chỉ biết diễn tả bằng 3 từ thôi: Quá tuyệt vời Con chưa từng thấy ai hiểu biết mà vẫn vô cùng quan tâm và biết lắng nghe, chia sẻ như cô Vân Anh. Kể cả sau 3 năm rồi, con vẫn cảm thấy rất an toàn khi luôn có 1 cô giáo nhiệt tình và thông thái như cô ở gần bên. "You are always there, teacher, and I don't really know how much I appreciate your help and guidance".