Trong bài này
Thuật ngữ cần chú ý
|
polynomial function (hàm số đa thức)
|
Hàm số có dạng f(x) = anxn + an-1xn-1 + ... + a1x + a0. |
|
quadratic function (hàm số bậc hai) |
Hàm số có dạng f(x) = ax2 + bx + c (a ≠ 0).
|
|
rational function (hàm số hữu tỉ) |
Hàm số có dạng f(x) = P(x)Q(x) (Q(x) ≠ 0).
|
|
intercept (điểm cắt trục)
|
Điểm mà đồ thị cắt trục Ox hoặc trục Oy
|
|
constant (hằng số) |
Giá trị không phụ thuộc vào bất kỳ yếu tố nào.
|
Dạng bài thường gặp
Cách 1: Sử dụng graphing calculator có sẵn trong bài thi SAT Math Digital
Hiện tại trong SAT Math Digital, các em sẽ được cung cấp một chiếc máy tính nằm sẵn trong giao diện bài thi có khả năng vẽ đồ thị từ phương trình cho trước. Các em có thể sử dụng nhập phương trình vào graphing calculator và sử dụng kết quả trùng khớp nhất để tìm ra đáp án.
Cách 2: Quan sát và đánh giá đồ thị/phương trình được cho trong đề bài
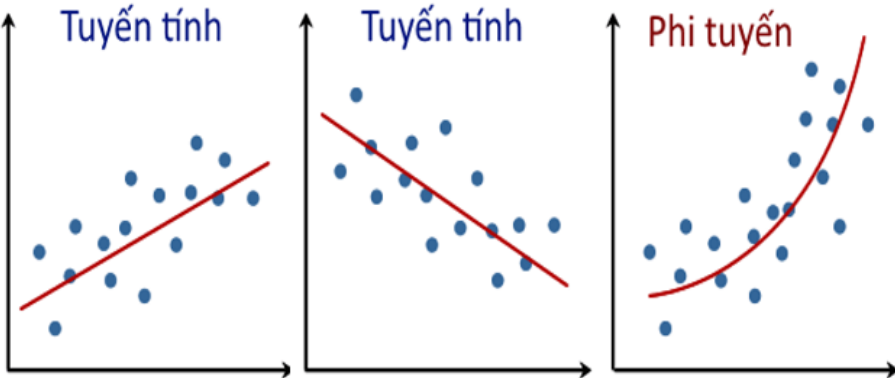
Bước 1: Tìm kiểu hàm số phi tuyến tính
- Xác định kiểu hàm số phi tuyến tính từ hình dáng của đồ thị hàm số.
- Ví dụ, nếu đồ thị là một parabol, thì hàm số có thể được biểu diễn dưới dạng f(x) = ax2 + bx + c.
- Đánh giá hệ số bậc cao nhất (leading coefficient) sẽ giúp ta tìm ra được hướng đi của đồ thị.
- Ví dụ, nếu hệ số bậc cao nhất của đồ thị mang dấu dương thì nhánh ngoài cùng bên phải của đồ thị phải đi lên.
- Ta thay lần lượt x=0 và y=0 vào phương trình của hàm số để tìm ra y-intercept và x-intercept tương ứng.
- Trong các phương trình đa thức, y-intercept chính là hệ số tự do (constant coefficient)
- Khi đó, đồ thị/phương trình nào thỏa mãn điều kiện về intercept sẽ là đáp án đúng.
- Từ đồ thị, chọn 1 điểm dễ dàng xác định tọa độ và thay vào phương trình
- Đồ thị/phương trình nào thỏa mãn sẽ là đáp án đúng.
Khi đề không cho sẵn phương trình mà mô tả một tình huống thực tế, các em cần tự lập hàm số bậc hai hoặc hàm số mũ từ lời văn — xem Các bài toán đố về hàm số bậc hai và hàm số mũ.
Đồ thị hàm số phi tuyến — bậc hai, mũ, đa thức — được học theo từng bài trong khoá Toán nâng cao trên HOCSAT Learn.
Bài tập
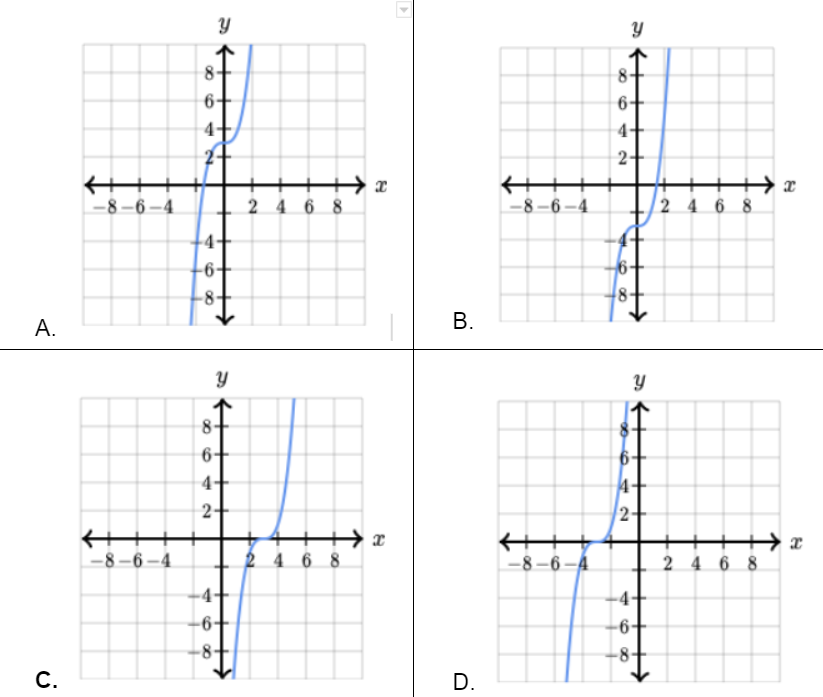
Đáp án: C
Bài 2: The graph of the polynomial equation y=a(t) is shown. Which of the following must be true?
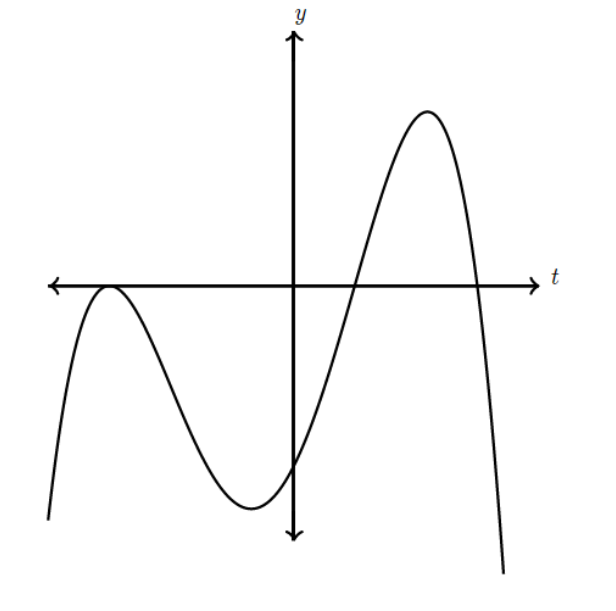
A) The leading coefficient is positive.
B) The sum of the distinct t‑intercepts is negative.
C) The constant coefficient is positive.
D) The product of the distinct t‑intercepts is negative.
Đáp án: C
