Các dạng cơ bản:
Trong bài thi, các em có thể được yêu cầu:
- Viết phương trình dựa trên bài toán đố
- Viết phương trình sau đó giải
- Giải một phương trình đã cho dựa trên bài toán đố
Công thức
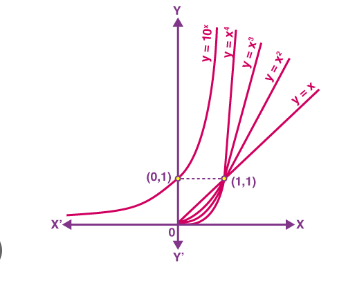
Các công thức khác nhau của hàm số bậc hai
Khi các em muốn biến đổi biểu thức bậc hai để xuất hiện điểm cắt trục y, chúng ta cần đưa biểu thức về dạng
a(x - b)2 + c, trong đó (b,c) chính là tọa độ vertex. Khi đó, biểu thức sẽ có giá trị lớn nhất (hoặc nhỏ nhất) bằng c khi x=b.
Khi các em muốn biến đổi biểu thức bậc hai để xuất hiện điểm cắt trục y, chúng ta cần đưa biểu thức về dạng
ax2 + bx + c, trong đó điểm (0,c) chính là y-intercept. Từ công thức này ta có thể tìm được hoành độ đỉnh: x = -b/2a
Khi các em muốn biến đổi biểu thức bậc hai để xuất hiện điểm cắt trục x, chúng ta cần đưa biểu thức về dạng
a(x - b)(x - c), trong đó (b,0) và (c,0) chính là x-intercept.
2. Công thức của hàm số mũ: y = abx
Trong đó:
a được gọi là constant (hằng số) hoặc initial value (giá trị ban đầu)
b được gọi là base (cơ số) hoặc factor (công bội)
x được gọi là exponent (số mũ) hoặc degree (bậc)
3. Biến đổi biểu thức hàm số mũ
Trong bài thi SAT, đôi khi đề bài sẽ đưa ra một biểu thức hàm số mũ sử dụng một đơn vị thời gian (ví dụ: năm) và yêu cầu các em viết lại biểu thức đó bằng một đơn vị thời gian khác (ví dụ: tháng).
a. Các bước làm bài
Bước 1: Xác định các đơn vị thời gian tương đương nhau được sử dụng cho câu hỏi.
Bước 2: Đảm bảo rằng hai biểu thức cho chúng ta các giá trị giống nhau khi sử dụng các đơn vị đó.
b. Ví dụ: Đề bài cho phương trình M = 100(1.62)
t, trong đó M là số thành viên của một câu lạc bộ sau khi mở cửa t năm và yêu cầu các em viết một phương trình mới thể hiện số lượng thành viên của câu lạc bộ sau khi mở m tháng.
Bước 1: Trong loại câu hỏi này, cơ số sẽ được giữ nguyên và chỉ có số mũ thay đổi. Chúng ta biết rằng số thành viên câu lạc bộ tăng theo hệ số 1.62 sau t = 1 năm, có nghĩa là số thành viên câu lạc bộ cũng cần tăng theo hệ số 1.62 sau m = 12 tháng.
Bước 2: Để đảm bảo số mũ của 1.62 là 1 khi m = 12, chúng ta cần chia m cho 12 theo số mũ:
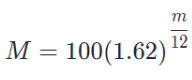
 Cách xử lý đề bài:
Cách xử lý đề bài:
Sau đây là ví dụ về cách xử lý dữ liệu đề bài toán đố:
A cable company with a reputation for poor customer service is losing subscribers at a rate of approximately 3% per year. The company had 2 million subscribers at the start of 2014.
Assume that the company continues to lose subscribers at the same rate, and that there are no new subscribers. Which of the following functions, S, models the number of subscribers (in millions) remaining t years after the start of 2014?
A. S(t) = 2(1.03)
t
B. S(t) = 2(0.97)
t
C. S(t) = 2(0.70)
t
D. S(t) = 2(0.97)
t
Hướng dẫn giải:
Khi đọc đề bài, các em sẽ thấy chúng ta được yêu cầu viết phương trình thể hiện số lượng người theo dõi còn lại sau t năm kể từ năm 2014. Hàm số ở đây chính là số lượng người theo dõi còn lại, được ký hiệu là S(t), biến số là số năm kể từ năm 2014, được ký hiệu là t.
Đề bài cho ta biết công ty có 2 triệu người theo dõi ở năm đầu tiên là năm 2014.
⇒ Các em tìm được initial value (giá trị ban đầu)
Ngoài ra, đề bài còn cho các em dữ kiện về việc mỗi năm công ty mất đi 3% người theo dõi. Như vậy cứ 1 năm trôi qua, số lượng người theo dõi sẽ bằng 100% - 3% = 97% hay 0.97 số lượng người theo dõi của năm trước đó.
⇒ Các em sẽ cần phải sử dụng hàm số mũ và 0.97 chính là factor (công bội).
⇒ Vậy phương trình hàm số cần tìm là S(t) = 2(0.97)
t.


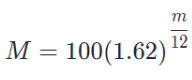


Trần Đình Quang (1560 SAT, THPT Chuyên Khoa Học tự nhiên) Trải nghiệm học SAT với TOEFL, con chỉ biết diễn tả bằng 3 từ thôi: Quá tuyệt vời Con chưa từng thấy ai hiểu biết mà vẫn vô cùng quan tâm và biết lắng nghe, chia sẻ như cô Vân Anh. Kể cả sau 3 năm rồi, con vẫn cảm thấy rất an toàn khi luôn có 1 cô giáo nhiệt tình và thông thái như cô ở gần bên. "You are always there, teacher, and I don't really know how much I appreciate your help and guidance".