Disable Preloader

Định lý đường tròn

Các em đã nắm rõ cách giải các bài toán liên quan tới định lý đường tròn trong các dạng Toán SAT chưa? Nếu chưa, hãy cùng theo dõi bài viết dưới đây để biết các chú ý về thuật ngữ, công thức cũng như thực hành một số bài tập liên quan nhé!

Mục lục bài viết

Các thuật ngữ cần chú ý

Thuật ngữ

 

Giải thích

 

Angle (Góc)

 

Phần mặt phẳng bị giới hạn bởi hai tia chung gốc

 

Vertex (Đỉnh)

 

Gốc chung của hai tia

 

Radian

Cung tròn có độ dài bằng bán kính gọi là cung có số đo 1 radian, gọi tắt là cung 1 radian. Góc ở tâm chắn cung 1 radian gọi là góc có số đo 1 radian, gọi tắt là góc 1 radian.

 

Acute angle (Góc nhọn)

 

Góc có số đo nhỏ hơn 90 độ.

 

Obtuse angle (Góc tù)

 

Góc có số đo lớn hơn 90 độ và nhỏ hơn 180 độ.

 

Right angle (Góc vuông)

 

Góc có số đo bằng chính xác 90 độ.

 

Straight angle (Góc bẹt)

 

Góc có số đo bằng chính xác 180 độ.

 

Complementary angles (Góc phụ nhau)

 

Hai góc phụ nhau có tổng số đo bằng 90 độ.

 

Supplementary angles (Góc bù nhau)

 

Hai góc bù nhau có tổng số đo bằng 180 độ.

 

Vertical angles (Góc đối đỉnh)

 

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh góc kia.

 

Arc (Cung)

 

Phần đường tròn bị giới hạn bởi hai điểm trên đường tròn.

 

Arc length (Độ dài cung)

 

Độ dài của đoạn thẳng được tạo ra từ cung.

 

Sector (Cánh quạt)

 

Một phần của hình tròn bị giới hạn bởi hai bán kính.

 

Circumference (Chu vi)

 

Tổng độ dài các cạnh của một hình.

 

Area (Diện tích)

 

Phần mặt phẳng bị giới hạn bởi các cạnh của hình.

 

Central angle (Góc ở tâm)

 

Góc được tạo bởi hai bán kính đường tròn.

 

Radius (Bán kính)

 

Khoảng cách từ tâm đường tròn đến một điểm bất kỳ nằm trên đường tròn.

 

Isosceles triangle (Tam giác cân)

 

Tam giác có hai cạnh bằng nhau.

 

Các công thức và tính chất liên quan tới định lý đường tròn

1. Chu vi đường tròn: C = 2𝝅r
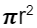
2. Diện tích hình tròn: A = Các công thức và tính chất liên quan tới định lý đường tròn 1
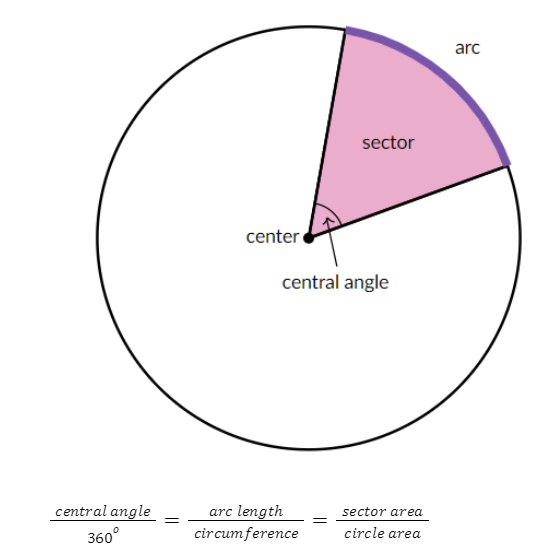
Các công thức và tính chất liên quan tới định lý đường tròn 2
3. Mối quan hệ giữa góc ở tâm, độ dài cung và diện tích cánh quạt
Ví dụ
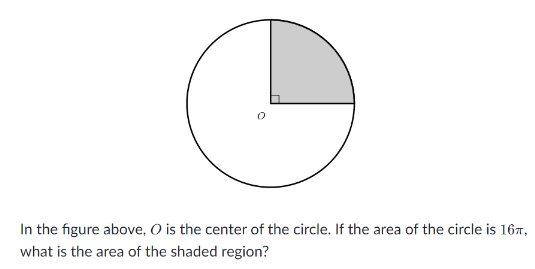
Các công thức và tính chất liên quan tới định lý đường tròn 3
Ta có: 
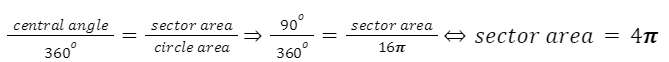
Các công thức và tính chất liên quan tới định lý đường tròn 4

4. Tổng số đo của tất cả các góc ở tâm bằng 360 độ.
5. Tam giác có hai cạnh là hai bán kính đường tròn là tam giác cân. Đây là một thông tin các em cần nhớ khi giải các bài toán liên quan tới định lý đường tròn.

Bài tập

Bài 1: (độ khó thấp)
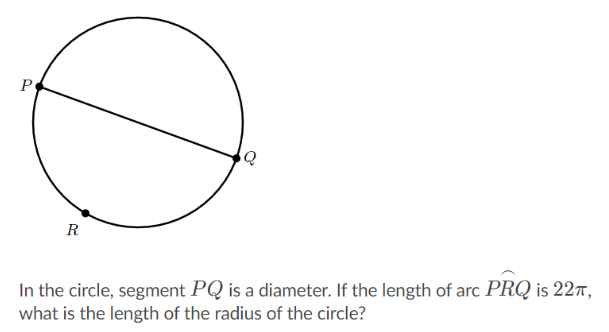
Bài tập 1
Đáp án: 22

Bài 2: (độ khó vừa)
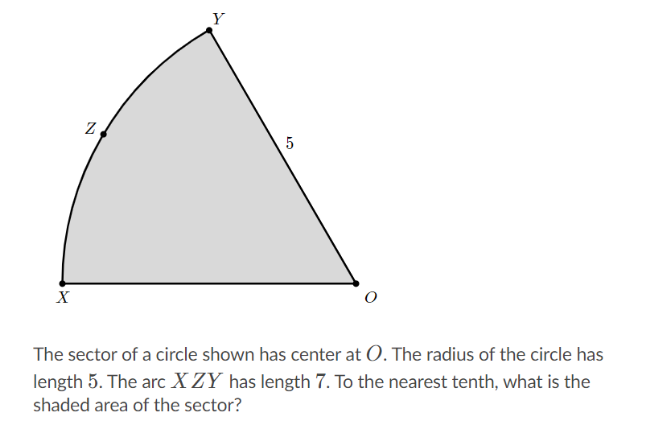
Bài tập 2
Đáp án: 17.5

Bài 3: (độ khó cao)
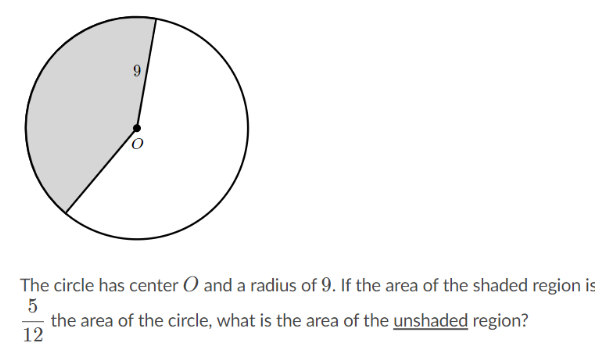
Bài tập 3

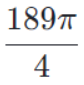
Đáp án: Bài tập 4
DMCA.com Protection Status

Để lại tin nhắn!

Tin cùng chuyên mục

Biểu đồ hộp
Biểu đồ hộp

Các em đã nắm rõ cách giải các bài toán về biểu đồ hộp trong Toán SAT chưa? Nếu chưa, hãy cùng theo ...

student's Feedback

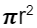
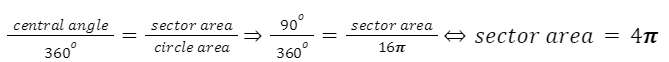
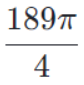
Trần Đình Quang (1560 SAT, THPT Chuyên Khoa Học tự nhiên) Trải nghiệm học SAT với TOEFL, con chỉ biết diễn tả bằng 3 từ thôi: Quá tuyệt vời Con chưa từng thấy ai hiểu biết mà vẫn vô cùng quan tâm và biết lắng nghe, chia sẻ như cô Vân Anh. Kể cả sau 3 năm rồi, con vẫn cảm thấy rất an toàn khi luôn có 1 cô giáo nhiệt tình và thông thái như cô ở gần bên. "You are always there, teacher, and I don't really know how much I appreciate your help and guidance".

học viên Trần Đình Quang
Trần Đình Quang
Chuyên Khoa Học tự nhiên.

Em thích nhất về độ thoải mái khi học, và sau mỗi buổi học đều cảm thấy rất có động lực học và được truyền cảm hứng. Em cảm thấy khoá học đáp ứng được đủ nhu cầu học SAT của em, lượng tài liệu đa dạng, đầy đủ và cách dạy của cô cũng rất dễ hiểu.

học viên Lê Minh Hiếu
Lê Minh Hiếu
Chuyên Ngoại Ngữ.

Em rất thích khóa học của cô Vân Anh, đặc biệt tài liệu của cô siêu siêu nhiều. Thi thoảng cô còn khao lớp trà trà/cafe mỗi lúc thấy lớp “đuối đuối” :D Lớp của em rất vui, sỹ số nhỏ nên em học được nhanh lắm, lộ trình học ngắn mà hiệu quả.

học viên Dương Nguyễn
Dương Nguyễn
THPT Chu Văn An.