
1. Tỷ lệ (Ratio):
a) Cách xác định tỷ lệ (ratio):
VD: Chúng ta có 5 quả táo, 7 quả cam. Chúng ta cần tìm ra tỷ lệ quả táo trên tổng số trái cây đã có.
Vậy ta có thể xác định:
- Số táo đã có là 5 quả
- Số trái cây đã có là: 5 quả táo + 7 quả cam = 12 quả
- Kết luận: Tỷ lệ táo đã có là: (Số táo)/(Số trái cây)= 5/12
b) Tìm tỉ số bù
Hai loại tỷ lệ phổ biến mà chúng ta thấy là tỷ lệ phần trên phần và tỷ lệ từng phần trên tổng số phần.
Ví dụ: Nếu chúng ta đang làm nước chanh:
- Tỷ lệ nước chanh với đường là tỷ lệ phần trên phần. Tỷ lệ này so sánh số lượng của hai thành phần.
- Tỷ lệ nước cốt chanh và nước chanh là tỷ lệ một phần tổng số. Tỷ lệ này so sánh số lượng của một thành phần với tổng của tất cả các thành phần.
Vì tất cả các thành phần cần phải cộng lại thành tổng, tỷ lệ giữa các thành phần và một phần trên toàn bộ thường bao hàm lẫn nhau. Điều này có nghĩa là chúng ta có thể sử dụng các tỷ lệ được cung cấp để tìm các tỷ lệ nào chúng ta cần để giải một bài toán!
Lưu ý: Giống như phân số có thể được đơn giản hóa, các tỷ lệ có thể được rút gọn hoặc mở rộng để tìm các tỷ lệ tương đương . Ví dụ, tỷ lệ 5/10 = 1/2.
2. Tỷ lệ thức (Proportion):
a) Cách xác định tỷ lệ (proportion):
VD: 9 cây bút có giá 11.50 đô-la. Vậy 7 cây bút có giá là bao nhiêu?
Vậy ta có thể xác định:
- x là giá của 7 cây bút.
- Vậy ta có tỷ lệ:
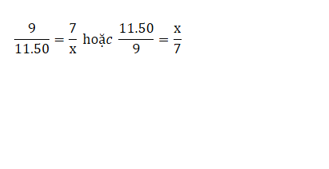
b) Giải các bài toán đố sử dụng tỉ lệ (proportion):
Nếu chúng ta biết một tỷ lệ và muốn áp dụng tỷ lệ đó cho một đại lượng khác, chúng ta có thể sử dụng tỷ lệ để thiết lập các tỷ lệ tương đương và tính toán bất kỳ đại lượng chưa biết nào.
Ví dụ: Giả sử chúng ta đang làm bánh quy và công thức yêu cầu
1 chén đường cho mỗi 3 chén bột. Nếu chúng ta muốn sử dụng 9 chén bột thì chúng ta cần bao nhiêu đường?
- Tỷ lệ đường/bột là 1:3.
- Tỷ lệ đường/bột theo yêu cầu có thể được viết là x:9.
- Để xác định lượng đường chúng ta cần, chúng ta có thể thiết lập tỷ lệ:
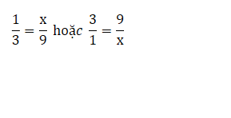 3. Tỷ lệ (Rate):
3. Tỷ lệ (Rate):
a) Cách xác định tỷ lệ (rate):
Ví dụ: Jayda mất 3 giờ để giao 189 tờ báo trên tuyến đường giao báo của mình. Tốc độ mỗi giờ mà cô ấy giao báo là bao nhiêu?
Vậy ta có thể xác định:
- x là số bút Jayda có thể giao trong 1 giờ.
- Vậy ta có tỷ lệ:
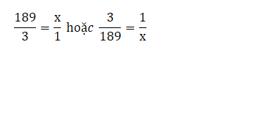
b) Áp dụng tỷ lệ trên mỗi đơn vị:
Tỷ lệ (Rate) được sử dụng để mô tả các đại lượng thay đổi như thế nào. Tỷ lệ phổ biến bao gồm tốc độ (khoảng cách/thời gian) và giá (tổng giá/ đơn vị đã mua).
Ví dụ, nếu chúng ta biết rằng một đoàn tàu đi 120 dặm trong 2 giờ, chúng ta có thể tính tốc độ trung bình của đoàn tàu trong hai giờ đó:
120/2 = 60 dặm/ 1 giờ.
Sau đó, chúng ta có thể sử dụng tốc độ đó để dự đoán các đại lượng khác, chẳng hạn như cùng một đoàn tàu đó, di chuyển với cùng tốc độ, sẽ đi được bao xa trong 5 dặm.
Lưu ý: Khi làm việc với tỷ lệ trong SAT, các em có thể cần thực hiện chuyển đổi đơn vị.
Bài 1: A bag is filled with red marbles and blue marbles. There are 54 total marbles in the bag, and 1/3 of the marbles are blue.
The ratio of blue marbles to total marbles is?
The ratio of red marbles to total marbles is?
The ratio of red marbles to blue marbles is?
How many red marbles are in the bag?
Đáp án: a) 1/3 b) 2/3 c) 2/1 d) 36
Bài 2: A local zoo houses 13 penguins for every lion it houses. The zoo houses 78 penguins. Which proportion(s) would allow us to solve for x, the number of lions housed at the zoo?

Đáp án: C
Bài 3: Tony buys 6 large pizzas for $77.94 before tax.
The price for a single large pizza is
The price of 10 large pizzas before tax would be
Đáp án: a) $12.99 b) $129.90



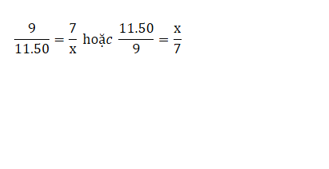
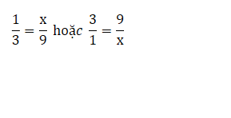
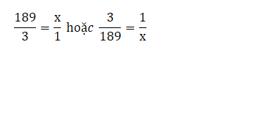



Trần Đình Quang (1560 SAT, THPT Chuyên Khoa Học tự nhiên) Trải nghiệm học SAT với TOEFL, con chỉ biết diễn tả bằng 3 từ thôi: Quá tuyệt vời Con chưa từng thấy ai hiểu biết mà vẫn vô cùng quan tâm và biết lắng nghe, chia sẻ như cô Vân Anh. Kể cả sau 3 năm rồi, con vẫn cảm thấy rất an toàn khi luôn có 1 cô giáo nhiệt tình và thông thái như cô ở gần bên. "You are always there, teacher, and I don't really know how much I appreciate your help and guidance".