Để giải hệ phương trình bậc nhất, chúng ta thường có 2 cách giải: thế và khử.
1. Phép thế
Để giải một hệ phương trình bằng phép thế:
- Cô lập một trong hai biến trong một trong các phương trình.
- Thay thế phương trình bằng biến cô lập từ Bước 1 vào phương trình khác. Ta có một phương trình bậc nhất chỉ có một biến.
- Giải phương trình bậc nhất để tìm biến đó và thế ngược vào phương trình để tìm biến còn lại.
y = 3x - 1
4x + y = 8
Ta có: y = 3x - 1, thế vào phương trình sau: 4x + (3x - 1) = 8 -> x = -1
Thế vào phương trình sau, ta có: 4(-1) + y =8 -> y = -4.
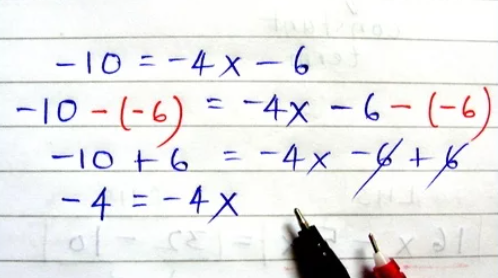 2. Phép khử
2. Phép khử
Để giải một hệ phương trình bằng phép khử:
- Xác định một cặp số hạng trong hệ có cùng biến và hệ số (ví dụ: 2y và 2y, 3x và -3x). Nếu không có, các em hãy biến đổi lại một hoặc cả hai phương trình sao cho một cặp số hạng có cùng biến và hệ số.
- Cộng hoặc trừ hai phương trình trong hệ để khử các số hạng đã xác định ở Bước 1. Các em sẽ có một phương trình bậc nhất chỉ có một biến.
- Giải phương trình bậc nhất để có được một giá trị cho biến.
- Bây giờ các em đã tìm ra giá trị của một biến, hãy thay giá trị đó vào một trong hai phương trình để tìm giá trị của biến còn lại.
VD: 3x + 2y = 10
2x - 2y = 5
Ta sẽ chọn khử biến 2y bằng cách cộng hai phương trình trong hệ với nhau, ta được:
5x = 15 -> x = 3.
Thể vào phương trình đầu, ta có:
3.3 + 2y = 10 -> y = 1/2.
 3. Cách xác định số nghiệm của hệ phương trình bậc nhất
3. Cách xác định số nghiệm của hệ phương trình bậc nhất
Ta có thể sử dụng phương pháp đồ thị, tuy nhiên, ở đây các em sẽ được hướng dẫn cách xác định bằng việc viết lại cả hai phương trình ở dạng hệ số góc-chặn, y = mx + b.
- Nếu hai phương trình có hệ số góc khác nhau thì hệ có một nghiệm.
- Nếu hai phương trình có cùng hệ số góc nhưng khác nhau hằng số, thì hệ vô nghiệm.
- Nếu hai phương trình có cả hai cùng hệ số góc và hằng số, thì hệ có vô số nghiệm.
Để xác định số lượng nghiệm của một hệ phương trình bậc nhất, sử dụng dạng hệ số góc-chặn, y = mx+b:
- Viết lại cả hai phương trình ở dạng hệ số góc-chặn.
- So sánh các hệ số góc và hằng số của phương trình để xác định số nghiệm.
VD: 1/3y = x + 2
y = 3x + 6
Các em có thể viết lại phương trình đầu tiên bằng cách nhân cả hai vế của phương trình đầu với 3:
y = 3x + 6
Vì phương trình thứ nhất trùng với phương trình thứ 2 nên hệ có vô số nghiệm.


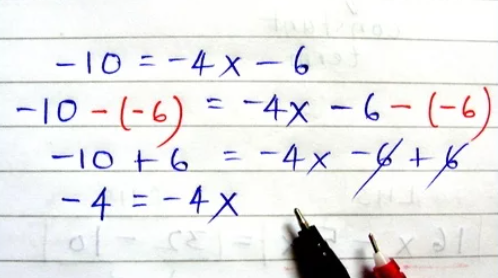


Trần Đình Quang (1560 SAT, THPT Chuyên Khoa Học tự nhiên) Trải nghiệm học SAT với TOEFL, con chỉ biết diễn tả bằng 3 từ thôi: Quá tuyệt vời Con chưa từng thấy ai hiểu biết mà vẫn vô cùng quan tâm và biết lắng nghe, chia sẻ như cô Vân Anh. Kể cả sau 3 năm rồi, con vẫn cảm thấy rất an toàn khi luôn có 1 cô giáo nhiệt tình và thông thái như cô ở gần bên. "You are always there, teacher, and I don't really know how much I appreciate your help and guidance".