Chia sẻ tài liệu SAT phần Toán
Phần toán SAT là phần mà nhiều bạn học sinh Việt Nam có thể tự ôn tập. Tài liệu ở phần toán này cũng...
Phương trình đường tròn
Các em đã nắm rõ cách giải các bài toán liên quan tới phương trình đường tròn trong các dạng Toán SAT chưa? Nếu chưa, hãy cùng theo dõi bài viết dưới đây để biết các chú ý về thuật ngữ, công thức cũng như thực hành một số bài tập liên quan nhé!
Các thuật ngữ cần chú ý
Các công thức phương trình đường tròn
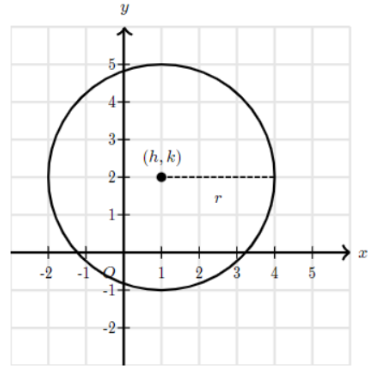
1. Phương trình đường tròn dạng chuẩn (standard form)
⇒ Tâm: (h;k)
Bán kính: r
2. Phương trình đường tròn dạng tổng quát (general form)
3. Sử dụng graphing calculator
Hiện nay ở trong giao diện bài thi SAT Math có tích hợp một máy tính có khả năng vẽ đồ thị hàm số từ phương trình cho trước. Em có thể nhập phương trình đường tròn đã cho và máy tính sẽ giúp em tìm ra tâm và bán kính.
Bài tập
Bài 1: (độ khó thấp) A circle equation is given as 
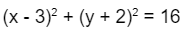
. Find the center and radius of that circle.
Đáp án: Center: (3;-2)
Radius: 4
Bài 2: (độ khó vừa) A circle equation is given below. Find the center and radius of that circle.
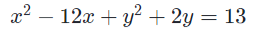
Đáp án:
Center: (6;-1)
Radius:
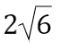
Bài 3: (nâng cao)
If all points on a circle are in Quadrant I in the xy-plane, which of the following could be the equation of the circle?
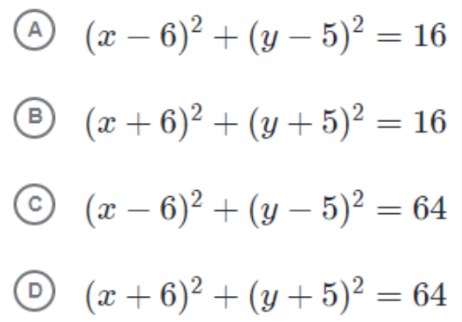
Đáp án: A
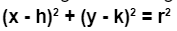
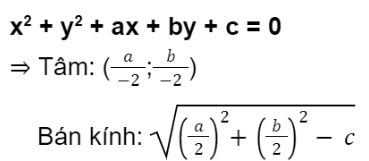
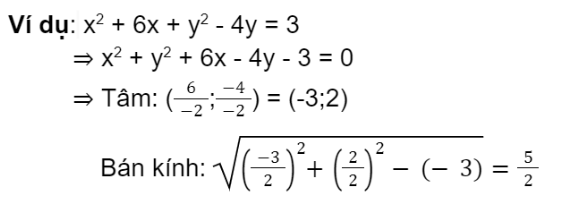
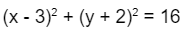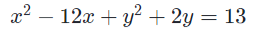
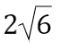
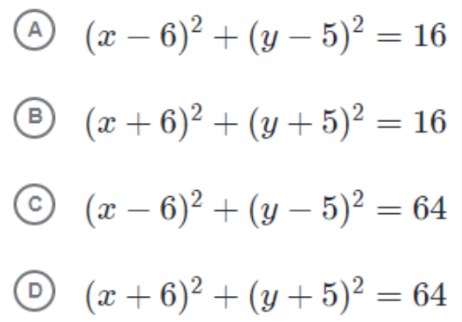
. Find the center and radius of that circle.Đáp án: Center: (3;-2)
Radius: 4
Bài 2: (độ khó vừa) A circle equation is given below. Find the center and radius of that circle.
Đáp án:
Center: (6;-1)
Radius:
Bài 3: (nâng cao)
If all points on a circle are in Quadrant I in the xy-plane, which of the following could be the equation of the circle?
Đáp án: A
Để lại tin nhắn!
Tin cùng chuyên mục
Biểu đồ hộp
Các em đã nắm rõ cách giải các bài toán về biểu đồ hộp trong Toán SAT chưa? Nếu chưa, hãy cùng theo ...
Phương trình chứa căn và phương trình hữu tỉ
Các em đã nắm rõ dạng bài về phương trình chứa căn và phương trình hữu tỉ trong Toán Digital SAT chư...
Các bài toán đố về hàm số bậc hai và hàm số mũ
Các bài toán đố về hàm số bậc hai và phương trình mũ là một trong những dạng khó trong Toán SAT digi...
Tính toán với biểu thức hữu tỉ
Các em đã nắm rõ cách thực hiện các thao tác tính toán với biểu thức hữu tỉ trong Toán SAT chưa? Nếu...
student's Feedback
Trần Đình Quang
Chuyên Khoa Học tự nhiên.
Em thích nhất về độ thoải mái khi học, và sau mỗi buổi học đều cảm thấy rất có động lực học và được truyền cảm hứng. Em cảm thấy khoá học đáp ứng được đủ nhu cầu học SAT của em, lượng tài liệu đa dạng, đầy đủ và cách dạy của cô cũng rất dễ hiểu.
Lê Minh Hiếu
Chuyên Ngoại Ngữ.
Em rất thích khóa học của cô Vân Anh, đặc biệt tài liệu của cô siêu siêu nhiều. Thi thoảng cô còn khao lớp trà trà/cafe mỗi lúc thấy lớp “đuối đuối” :D Lớp của em rất vui, sỹ số nhỏ nên em học được nhanh lắm, lộ trình học ngắn mà hiệu quả.
Trần Đình Quang (1560 SAT, THPT Chuyên Khoa Học tự nhiên) Trải nghiệm học SAT với TOEFL, con chỉ biết diễn tả bằng 3 từ thôi: Quá tuyệt vời Con chưa từng thấy ai hiểu biết mà vẫn vô cùng quan tâm và biết lắng nghe, chia sẻ như cô Vân Anh. Kể cả sau 3 năm rồi, con vẫn cảm thấy rất an toàn khi luôn có 1 cô giáo nhiệt tình và thông thái như cô ở gần bên. "You are always there, teacher, and I don't really know how much I appreciate your help and guidance".