Thuật ngữ
|
Thuật ngữ
|
Giải thích
|
|
Similar triangles (Tam giác đồng dạng)
|
Các tam giác được gọi là đồng dạng nếu chúng có 3 góc tương ứng (corresponding angles) bằng nhau và 3 cạnh tương ứng (corresponding sides) tỉ lệ.
|
|
Congruent triangle (Tam giác bằng nhau)
|
Các tam giác được gọi là bằng nhau nếu tất cả các số đo của chúng đều bằng nhau.
|
|
Scale factor (Hệ số tỷ lệ)
|
Tỷ lệ độ dài các cạnh tương ứng của các hình đồng dạng.
|
|
Hypotenuse (Cạnh huyền)
|
Cạnh dài nhất trong tam giác vuông, nằm đối diện với góc vuông.
|
|
Leg (Cạnh góc vuông)
|
Trong một tam giác vuông (right triangle), hai cạnh tạo với nhau một góc 90 độ được gọi là hai cạnh góc vuông.
|
|
Isosceles triangle (Tam giác cân)
|
Tam giác có hai cạnh bằng nhau.
|
|
Equilateral triangle (Tam giác đều)
|
Tam giác có ba cạnh bằng nhau.
|
Năm cách chứng minh tam giác bằng nhau
SSS (Side-Side-Side): Nếu ba cạnh của tam giác này bằng ba cạnh của tam giác kia thì hai tam giác đó bằng nhau.
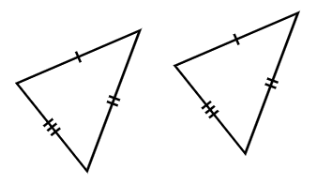
SAS (Side-Angle-Side): Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
.png)
ASA (Angle-Side-Angle): Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
.png)
AAS (Angle-Angle-Side): Nếu một cạnh và hai góc của tam giác này bằng một cạnh và hai góc của tam giác kia thì hai tam giác đó bằng nhau.
.png)
HL (Hypotenuse-Leg, right triangle only): Nếu cạnh huyền và cạnh góc vuông của tam giác vuông này bằng cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
.png)
Ba cách chứng minh tam giác đồng dạng
AA (Angle-Angle): Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng với nhau.
VD: Tam giác DEF có góc DEF = 40 độ, EDF = 50 độ và tam giác D’E’F’ có góc D’E’F’ = 40 độ, E’D’F’ = 50 độ thì 2 tam giác này được coi là đồng dạng.
.png)
SSS (Side-Side-Side): Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng với nhau.
VD: Tam giác MNP có MN = 3cm, NP = 4cm và góc MNP = 60 độ. Tam giác M’N’P’ có M’N’ = 6cm, N’P’ = 8cm và góc M’N’P’ = 60 độ thì 2 tam giác này đồng dạng với nhau.
.png)
SAS (Side-Angle-Side): Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đồng dạng với nhau
VD: Tam giác MNP có MN = 3cm, NP = 4cm và góc MNP = 60 độ. Tam giác M’N’P’ có M’N’ = 6cm, N’P’ = 8cm và góc M’N’P’ = 60 độ thì 2 tam giác này đồng dạng với nhau
.png)
Tìm độ dài các cạnh chưa biết trong các tam giác đồng dạng
.png)
Để tính chiều dài cạnh bị thiếu, các em cần thực hiện 3 bước sau:
Bước 1: Viết biểu thức tỉ lệ của ba cặp cạnh tương ứng.
.png)
Bước 2: Thay độ dài các cạnh đã biết vào biểu thức. Chúng ta cần biết 3 trong số 4 độ dài cạnh để tính độ dài cạnh còn thiếu.
Bước 3: Tìm độ dài cạnh còn thiếu.
Ví dụ
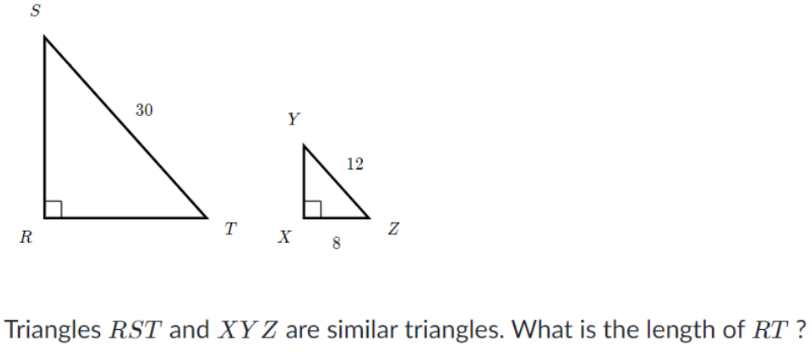
Đề bài cho các em dữ kiện: 2 tam giác RST và XYZ là 2 tam giác đồng dạng và yêu cầu các em đi tính độ dài cạnh RT.
Bước 1:
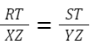
Bước 2: Thay số:
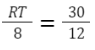
Bước 3: RT = 20
Bài tập
Bài 1 (độ khó thấp): Triangles ABC and DEF are shown above. If the two triangles are congruent, which of the following statements must be true?
.png)
A. ∠A and ∠B have the same measure.
B. ∠A and ∠E have the same measure.
C. AC and BC have the same length.
D. AB and DE have the same length.
E. AC and DE have the same length.
Đáp án: D
Bài 2 (độ khó vừa): Calculate the values of unknown lengths.
.png)
Đáp án: x = 10, y = 8
Bài 3 (độ khó cao): In the diagram, ∠POR = ∠QRS = ∠RST = 90°, PQ = QR = RS = 5 cm and ST = 1cm. Find the length of QU.
.png)
Đáp án: 3




.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
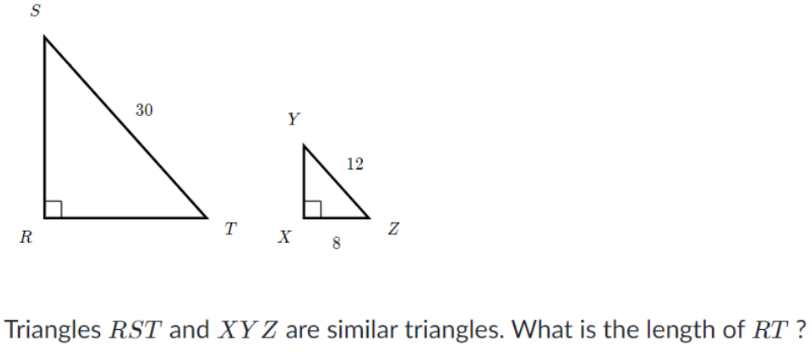
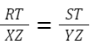
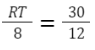
.png)
.png)
.png)

Trần Đình Quang (1560 SAT, THPT Chuyên Khoa Học tự nhiên) Trải nghiệm học SAT với TOEFL, con chỉ biết diễn tả bằng 3 từ thôi: Quá tuyệt vời Con chưa từng thấy ai hiểu biết mà vẫn vô cùng quan tâm và biết lắng nghe, chia sẻ như cô Vân Anh. Kể cả sau 3 năm rồi, con vẫn cảm thấy rất an toàn khi luôn có 1 cô giáo nhiệt tình và thông thái như cô ở gần bên. "You are always there, teacher, and I don't really know how much I appreciate your help and guidance".